Math Help for Section 3.6, Page 144

Intervals
on the Real Number Line
Inequalities that
contain one or more variable terms, such as 

    $x\le 4$,  
 $x\ge -3$,  
 $x+2>7$,  
 and    $4x-6<3x+8$,

are called algebraic
inequalities.

    Be sure you understand the
difference between $ < $ and $ \le $ and the difference between
$>$ and $\ge$. For instance, consider the inequalities $x
> 5$ and $x \ge 5.$ The solution set of $x > 5$ consists
of all real numbers that are greater than 5, but excludes the
number 5 itself. It is graphed as follows.

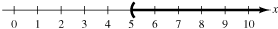
The solution set of $x \ge 5$ consists of all real numbers
that are greater than 5 and includes the number 5 itself. It is graphed as
follows.

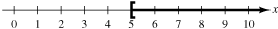
Study
Tip
When a and b are real numbers, the lengths of $[a,\,b]$, $(a,\,b)$, $[a,\,b)$, and $(a,\,b]$ are the
same. The reason that these
four types of intervals are called “bounded” is that each has a finite
length. An
interval that does not
have a finite length is unbounded
(or infinite).
Unbounded intervals are discussed on page 79.