Math Help for Section 3.6, Page 148
Solving
Linear Inequalities
A compound inequality formed by the word and is called conjunctive and is
the only kind that has the potential to form a double inequality. A
compound
inequality joined by the word or
is called disjunctive
and cannot be re-formed
into a double inequality.
Example
6: Tip
The double inequality in Example 6 could have been solved in two parts,
as
follows.
| $-7\le 5x-2$ | and | $5x-2<8\;$ | |||
| $-5\le 5x$ | $5x<10$ | ||||
| $-1\le x$ | $x<2\;$ |
The solution set consists of all real numbers that satisfy both
inequalities. In other
words, the solution set is the set of all values of x for which
$-1\le x<2$.
The solution set in set notation is $\{x|-1\le x<2\}$.
Study
Tip
Compound inequalities can be written using symbols. For
compound
inequalities,
the word and
is represented by the symbol $\cap$, which is read as
intersection.
The word or
is represented by the symbol $\cup$, which is read as union.
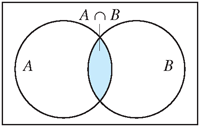
Graphical
representations are shown in the figures below. If A and B are sets, then x
is in $A\cap B$ if
it is in both A
and B.
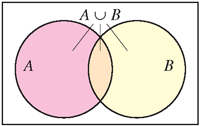
Similarly, x
is in $A\cup B$ if it is in A,
B, or both A
and B.
|
|
|
| Intersection of two sets | Union of two sets |
Example
7: Tip
The solution set in set notation is $\{x|x\le
-{1\over3}\}\cup\{x|x\ge {4\over3}\}$.
Study
Tip
The
following tips describe how to solve compound inequalities in a few
special situations. Try graphing the examples on a number line to
better understand the solutions.
| Tip | Example | Solution | |||
|
When you solve a compound inequality formed by the word and and you get two inequalities with one contained in the other, the solution is the inequality that is contained in the other. |
$x>-2$ and $x>4$ |
$x>4$ | |||
| When you solve a compound inequality formed by the word and and you get two inequalities with no values in common, the compound inequality has no solution. |
$x\le 0$ and $x>5$ |
No solution | |||
| When you solve a compound inequality formed by the word or and you get two inequalities that, together, contain the whole set of real numbers, the solution is all real numbers. |
$x<3$ or $x\ge 1$ | $-\infty<x <\infty$ |