Math Help for Section 3.1, Page 102
Solving
Linear Equations in Standard Form
In the first two chapters, you were introduced to the rules of algebra,
and you learned to use these rules to rewrite and simplify algebraic
expressions. In Sections 2.3 and 2.4, you gained experience in
translating verbal phrases and problems into algebraic expressions and
equations. You are now ready to use these skills and experiences to
solve linear equations
in one variable.
A linear equation in one
variable is also called a first-degree
equation because its variable has an implied exponent of
1 $\left( {x = {x^1}} \right).$ Here are
some examples of linear equations in standard form.
| $2x = 0$ | $4x + 6 = 0$ |
| $x – 7 = 0$ | $\displaystyle{x \over 2} – 1 = 0$ |
Remember that to solve
an equation involving x
means to find
all values of x
that satisfy the equation. For the linear equation $ax + b = 0,$ the
goal is to isolate x
by rewriting the equation in the form
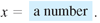
Isolate
the variable x.
To obtain this form, you use the techniques discussed in
Section 2.4. That is, you begin with the original equation and use the
Properties of Equality from page 88 to eliminate terms or factors until
you isolate the variable. For instance, to solve the linear equation $x
– 2 = 5,$
you can add 2 to each side of the equation to obtain $x = 7.$ As
mentioned in
Section 2.4, each equivalent equation is called a step of the
solution.
Example
1: Tip
Solving an equation has two basic stages. The first stage is to find
the solution (or solutions). The second stage is to check that each
solution satisfies the original equation. You can
improve your accuracy in algebra by developing the habit of checking
each solution.
While completing the first stage, a common question in algebra is
first to
isolate x?”
The answer is that you need practice. By solving many linear
equations, you will find that your skill will improve. The key thing to
remember is that you can “get rid of” terms and factors by using inverse operations.
Here are some guidelines and examples.
| Guideline | Equation | Inverse Operation | |
| Subtract to remove a sum. |
$x + 3 = 0$ | Subtract 3 from each side. |
|
| Add to remove a difference. |
$x – 5 = 0$ | Add 5 to each side. |
|
| Divide to remove a product. |
$4x = 20$ | Divide each side by 4. |
|
| Multiply to remove a quotient. |
$\displaystyle{x \over 8} = 0$ | Multiply each side by 8. |
Here is how you could use this technique in Example 1.
| Guideline | Equation | Inverse Operation | |
| Add to remove a difference. | $3x – 15 = 0$ | Add 15 to each side. | |
| Divide to remove a product. | $3x = 15$ | Divide each side by 3. |
For additional examples, review Example 4 on page 89. Note how inverse operations are used to isolate
the variable.