Math Help for Section 3.3, Page 122

Markups
and Discounts
The amount a retailer pays for the item is called the cost. The amount at
which the retailer sells the item to the consumer is called the price. Markup is the
difference between price and cost. Varying markups are the reason for
different prices for an item at different stores. Markup is one of
those “hidden operations” referred to in Section 2.3.

If you solve the selling price model for markup, you get the following
equivalent model.

If you substitute the model

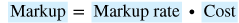
into the model

    , 

you get the following model for selling price, in terms of
cost and markup rate.

This is the model shown in the solution of part (c) of Example
6.

Example
6: Tip

Here are intermediate steps for getting from the model to the equation.

a.	Verbal Model:
	Labels:	${\text{Selling price}} = x$	(dollars)
		${\text{Cost}} = 45$	(dollars)
		${\text{Markup rate}} = 0.55$	(decimal form)
		${\text{Markup}} = \left( {0.55} \right)\left( {45} \right)$	(dollars)
	Equation:	${\text{Selling price}} = {\text{45}} + \left( {0.55} \right)\left( {45} \right)$
b.	Verbal Model:
	Labels:	${\text{Selling price}} = 98$	(dollars)
		${\text{Cost}} = C$	(dollars)
		${\text{Markup rate}} = 0.60$	(decimal form)
		${\text{Markup}} = 0.6c$	(dollars)
	Equation:	$98 = C + 0.6C$
c.	Verbal Model:
	Labels:	${\text{Selling price}} = 60$	(dollars)
		${\text{Cost}} = 24$	(dollars)
		${\text{Markup rate}} = p$	(decimal form)
	Equation:	$60 = 24 + p\left({24} \right)$

Example 6: Check

$\eqalign{{\textbf{a.}\quad\text{Selling price}
} =& {\text{45}} + \left( {0.55} \right)\left(
{45} \right)&{\small\color{red}\quad\quad\text{Write
original equation.}} \cr \color{red}69.75\color{black}
\overset{?}{=}& 45 + 0.55\left({45}
\right)&{\small\color{red}\quad\quad\text{Substitute 69.75
for Selling price.}}  \cr 69.75
\overset{?}{=}& 45
+ 24.75&{\small\color{red}\quad\quad\text{Multiply.}} \cr 69.75
=& 69.75&{\small\color{red}\quad\quad\text{Solution
checks. }\checkmark}\cr} $

$\eqalign{{\textbf{b.}\quad}98 =& C +
0.6C&{\small\color{red}\quad\quad\text{Write original 
equation.}} \cr 98\overset{?}{=}&
\color{red}61.25\color{black} + 0.6\left(
{\color{red}61.25}\right)&{\small\color{red}\quad\quad\text{Substitute
61.25 for }C.} \cr
98\overset{?}{=}& 61.25 +
36.75&{\small\color{red}\quad\quad\text{Multiply.}} \cr
98 =& 98&{\small\color{red}\quad\quad\text{Solution
checks. } \checkmark} \cr} $

$\eqalign{{\textbf{c.}\quad} 60 =& 24 + p\left( {24}
\right)&{\small\color{red}\quad\quad\text{
Write original
equation.}} \cr 60\overset{?}{=}& 24 + \left( {\color{red}1.5}
\right)\left( {24}
\right)&{\small\color{red}\quad\quad\text{Substitute 1.5
for }p.} \cr
60\overset{?}{=}& 24 +
36&{\small\color{red}\quad\quad\text{Multiply.}} \cr 60
=&
60&{\small\color{red}\quad\quad\text{Solution checks. }\checkmark}
\cr}$