Math Help for Section 3.6, Page 144
Intervals
on the Real Number Line
Inequalities that
contain one or more variable terms, such as
$x\le 4$,
$x\ge -3$,
$x+2>7$,
and $4x-6<3x+8$,
are called algebraic
inequalities.
Be sure you understand the
difference between $ < $ and $ \le $ and the difference between
$>$ and $\ge$. For instance, consider the inequalities $x
> 5$ and $x \ge 5.$ The solution set of $x > 5$ consists
of all real numbers that are greater than 5, but excludes the
number 5 itself. It is graphed as follows.
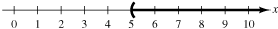
The solution set of $x \ge 5$ consists of all real numbers
that are greater than 5 and includes the number 5 itself. It is graphed as
follows.
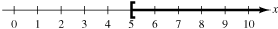
Study
Tip
When a and b are real numbers, the lengths of $[a,\,b]$, $(a,\,b)$, $[a,\,b)$, and $(a,\,b]$ are the
same. The reason that these
four types of intervals are called “bounded” is that each has a finite
length. An
interval that does not
have a finite length is unbounded
(or infinite).
Unbounded intervals are discussed on page 79.